In the algorithm problem solving every morning, it took time, but I solved two problems.
This time, it was easy except that it took a long time because ‘//’ and ‘%’ were confused with each other in division.

'n' Numbers Spaced by 'x'

• The function solution should take an integer ‘x’ and a natural number ‘n’, and return a list containing ‘n’ numbers, starting at ‘x’ and increasing by ‘x’.

def solution(x, n):
    answer = []
    for i in range(1, n + 1):
        answer.append(x * i)

    return answer

Find the Number Whose Remainder is 1

• A natural number n is given as a parameter. Complete the solution function to return the smallest natural number ‘x’ such that the remainder when ‘n’ is divided by ‘x’ is 1.

def solution(n):
    x = 0
    while True:
        x += 1
        if n % x == 1:
            break
    return x

And I feel that the class I am currently taking is very difficult.
After understanding and actually applying it, it takes about 4 hours to listen to the lecture for about 30 minutes.

For example, the following problem.

Find the Alphabet

• Given a word S made up of only lowercase letters of the alphabet. Write a program that outputs the position of the first occurrence of each letter if it is included in the word, or -1 if it is not included.
• For each alphabet, the position where a first appears, the position where b first appears, … the position where z first appears are separated by spaces and output.
• If an alphabet is not included in the word, -1 is output. The first letter of the word is position 0, the second letter is position 1.

As you can see from the above, it took me a while to understand the problem…

import string


def get_idx_naive(word):
    result = [-1]*len(string.ascii_lowercase)
    for i in range(len(word)):
        char = word[i]
        for j in range(len(string.ascii_lowercase)):
            lo = string.ascii_lowercase[j]
            if result[j] == -1 and char == lo:
                result[j] = i
    print(' '.join([str(num) for num in result]))


get_idx_naive('baekjoon')

To solve this problem, first create a ‘list’ full of ‘-1’s and compare them.
If you start with this idea, you can write code by putting ‘for’ inside ‘for’.

This is O(N^2) but you can reduce to O(N) using ASCII code.

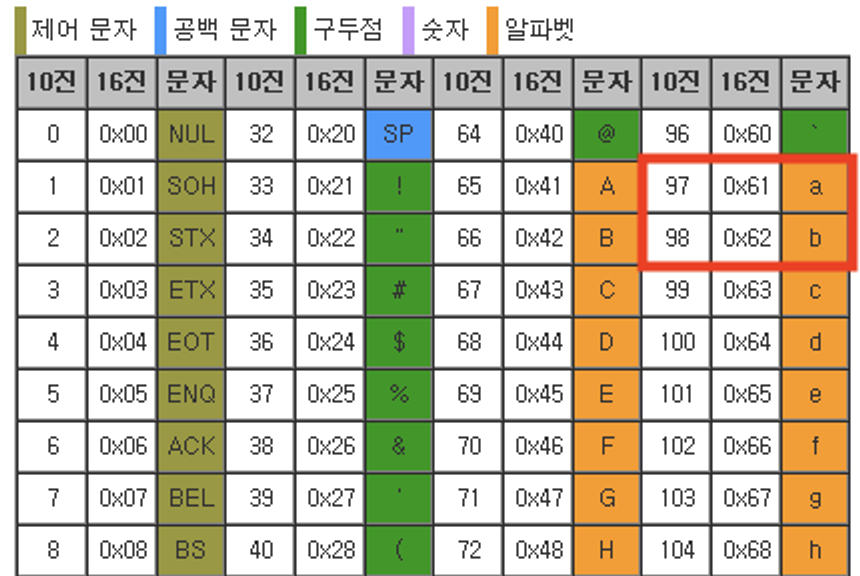
import string


def get_idx(word):
    # point 1. ord
    # point 2. O(n^2) -> O(n)
    result = [-1]*len(string.ascii_lowercase)
    for i in range(len(word)):
        idx = ord(word[i]) - 97
        if result[idx] == -1:
            result[idx] = i
    print(' '.join([str(num) for num in result]))

get_idx('baekjoon')

Comparing with a ‘list’ of ‘-1’ is the same, but using ‘ord’ converts a character to a number so that ‘for’ can be used only once.

This is an algorithmic problem that gets more difficult the more you know. I have to dig really hard.